Counter-Ant System (CAS): A Simple Way to Learn Swarm Intelligence for Structural Design
- Adisorn O.
- Oct 1
- 4 min read
Cite as:
Adisorn Owatsiriwong (2025). Counter-Ant System (CAS): A Simple Way to Learn ACO (https://www.mathworks.com/matlabcentral/fileexchange/182184-counter-ant-system-cas-a-simple-way-to-learn-aco), MATLAB Central File Exchange. Retrieved October 1, 2025.
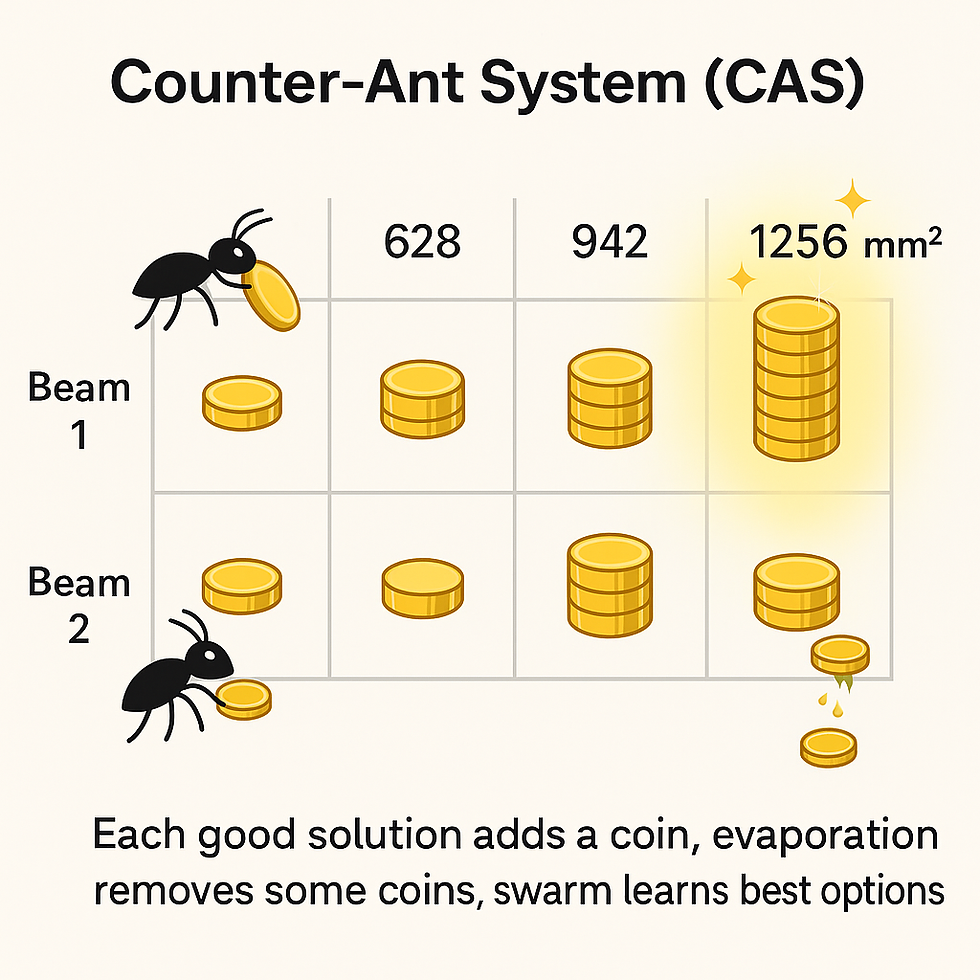
When engineers first hear about Ant Colony Optimization (ACO), it sounds complicated. Pheromone trails, probabilistic choices, heuristic factors — it’s easy to feel lost in the biology.
But what if we strip it down to its essence?
That’s where the Counter-Ant System (CAS) comes in.
🐜 The Core Idea
Instead of thinking of pheromone as mysterious equations, think of it as counters or votes:
Each design variable (e.g., each beam) has a set of options (rebar sizes).
Whenever a safe and feasible solution is built, the chosen options each get +1 vote.
Old votes gradually fade away (evaporation).
Over many iterations, the options with the most votes rise to the top, guiding the search toward the best design.
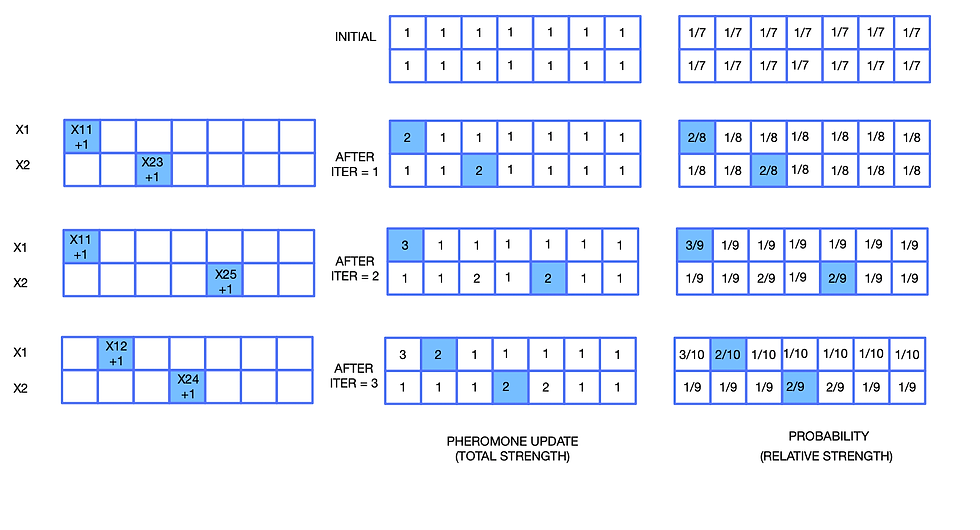
🔄 Iterative Learning
At every iteration:
Ants build designs based on current votes.
Unsafe designs are discarded.
Votes decay slightly (forgetting old, possibly wrong choices).
Feasible designs add fresh votes.
Over time, the swarm converges to the lightest safe total As across both beams.
📈 Why CAS Works
Easy to understand: no heavy equations, just counting.
Exploration & exploitation balance: random choices explore, votes exploit.
Evaporation: ensures old mistakes don’t dominate forever.
Extendable: once you’re comfortable, you can enhance it by weighting votes with design quality (e.g., Q/cost).
✅ Takeaway
The Counter-Ant System (CAS) is a friendly introduction to swarm intelligence for engineering optimization. It captures the essence of Ant System — memory, fading trails, collective search — in a way that’s simple enough to implement in a few lines of MATLAB code.
And the best part?
Even this stripped-down version is powerful enough to solve small but real problems, like multi-beam rebar design.
PSEUDO CODE
INPUT:
V = number of variables (e.g. beams, columns)
O[v] = list of discrete options for variable v
EVALUATE(X) = returns (cost, feasible) for full solution X
m = number of ants
maxIter = number of iterations
rho = evaporation rate (0 < rho < 1)
INITIALIZE:
tau[v][j] = 1 # pheromone counters for all options
bestCost = +infinity
bestSolution = null
FOR iter = 1..maxIter
# --- Ants build solutions ---
FOR k = 1..m
X = []
FOR each variable v
# Probability proportional to current counters
probs[j] = tau[v][j] / sum(tau[v][:])
choice = ROULETTE_SELECT(probs)
X[v] = choice
END
(cost, feasible) = EVALUATE(X)
IF not feasible THEN cost = +infinity
SAVE (X, cost)
IF cost < bestCost THEN
bestCost = cost
bestSolution = X
END
END
# --- Pheromone update ---
FOR each v,j
tau[v][j] = (1 - rho) * tau[v][j] # evaporation
END
FOR each ant k with finite cost
FOR each variable v
j = X_k[v]
tau[v][j] = tau[v][j] + 1 # add one vote
END
END
RECORD bestCost for convergence curve
END
OUTPUT:
bestSolution, bestCost⚙️ Example: 2-Beam Rebar Design
Imagine two beams that need flexural reinforcement:
Beam 1 demand: 100 kNm
Beam 2 demand: 150 kNm
Rebar options: As = {402, 628, 942, 1256 mm²}
Each “ant” (a trial design) picks one rebar size for each beam.
If the design is safe → add +1 vote to those chosen options.
If unsafe → no votes are added.
Meanwhile, all votes decay by 10% each round (ρ = 0.1).
This way, only the options that keep showing up in good designs remain strong.

MATLAB CODE
function SimpleAS_Counter_Evap()
close all
clc
clear
% --- Problem Setup ---
As_list = [402, 628, 942, 1256]; % rebar areas (mm2)
nOptions = numel(As_list);
nVars = 2; % 2 beams
Mu = [100e6, 150e6]; % demands for beams (Nmm)
fy = 400; d = 500; % material, mm
% --- Parameters ---
nAnts = 2; nIter = 20;
alpha = 1;
rho = 0.1; % evaporation rate
% --- Pheromone (start as counters = 1) ---
tau = ones(nVars,nOptions);
% Track best
bestCost = inf; bestSol = [];
conv = zeros(1,nIter);
for iter = 1:nIter
solutions = zeros(nAnts,nVars);
costs = inf(1,nAnts);
% --- Ants construct solutions ---
for k = 1:nAnts
choice = zeros(1,nVars);
for v = 1:nVars
% Probabilities depend on pheromone (counters with decay)
probs = tau(v,:).^alpha;
probs = probs/sum(probs);
r = rand; cumP = cumsum(probs);
choice(v) = find(r <= cumP,1,'first');
end
% Evaluate full solution
As_beam = As_list(choice);
safe = true;
for v = 1:nVars
Mn = 0.87*fy*As_beam(v)*d;
if Mn < Mu(v), safe=false; end
end
if safe
cost = sum(As_beam);
else
cost = inf;
end
solutions(k,:) = choice;
costs(k) = cost;
if cost < bestCost
bestCost = cost; bestSol = choice;
end
end
% --- Pheromone update with evaporation ---
tau = (1-rho)*tau; % fade old votes
for k = 1:nAnts
if costs(k) < inf
for v = 1:nVars
tau(v,solutions(k,v)) = tau(v,solutions(k,v)) + 1; % add 1 vote
end
end
end
conv(iter) = bestCost;
fprintf('Iter %d | Best cost = %.0f | Tau = %s\n',...
iter,bestCost,mat2str(tau,3));
end
% --- Results ---
fprintf('\n=== Final Result ===\n');
disp(['Best solution indices: ',mat2str(bestSol)]);
disp(['Rebar areas: ',mat2str(As_list(bestSol))]);
disp(['Total As = ',num2str(bestCost),' mm2']);
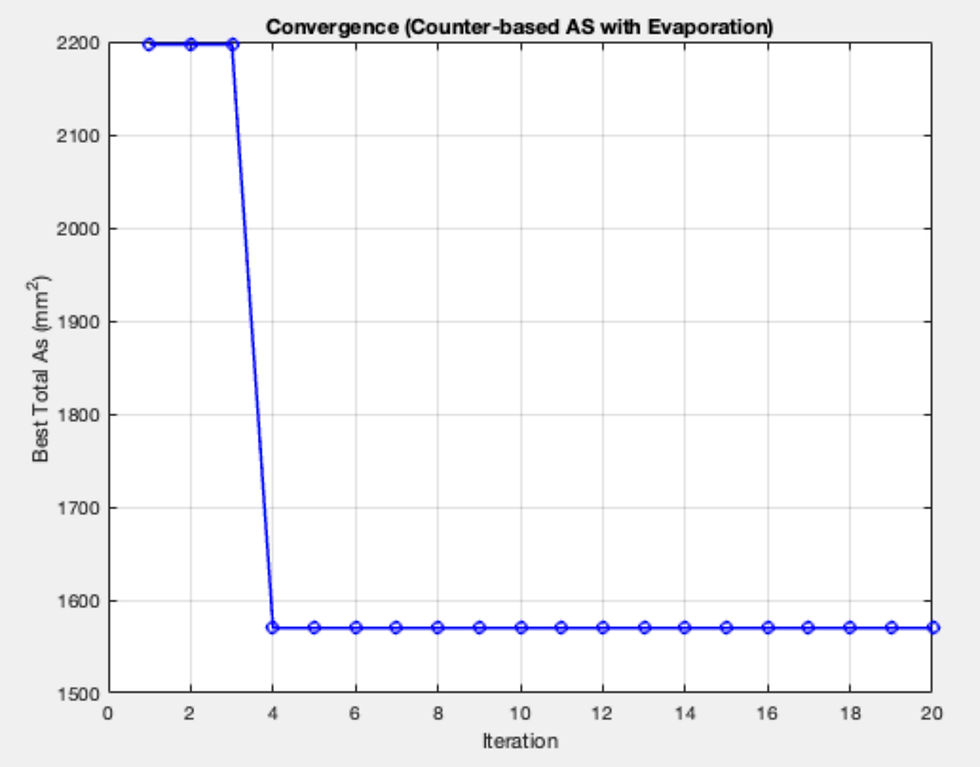
% --- Convergence plot ---
figure;
plot(1:nIter,conv,'b-o','LineWidth',1.5);
xlabel('Iteration'); ylabel('Best Total As (mm^2)');
title('Convergence (Counter-based AS with Evaporation)');
grid on;
end
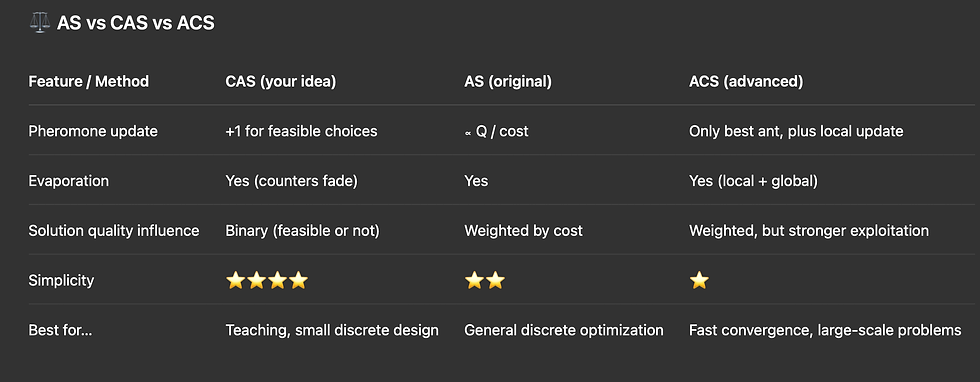
Closure :
In structural optimization problems, feasibility constraints and reinforcement (pheromone) dominate the search. The heuristic term provides only marginal acceleration, so a simplified Counter-Ant System (CAS) without heuristics is adequate and easier to apply.



