Multi-Objective Optimization using PSO (MOPSO)--Spread Footing Design Example

Problem setup

We want to design a square footing on soil that satisfies safety and economy.

• Design variables:

  
  

  • B = footing width (m)

  • D = embedment depth (m)

  
  

• Objectives (two conflicting goals):

  
  

  1. Minimize cost

     f_1 = Ccx B^2 xD

     where Cc is unit cost of concrete per m³ (say 100 USD/m³).

  2. Maximize bearing capacity safety (equivalent to minimizing failure risk)

     For safety, we want large factor of safety (FS), but since MOPSO is minimization-oriented, we set:

     f2 = 1/FS

     with

     FS = q_ult/q_applied

  
  

• Bearing capacity (Terzaghi’s equation for square footing):

  q_ult = 1.3 c x N_c + gamma xD x N_q + 0.4 gamma xB x N_gamma

  where

  
  

  • c = soil cohesion (kPa),

  • gamma = unit weight (kN/m³),

  • N_c, N_q, N_gamma = Terzaghi's bearing capacity factors (from phi),

  • q_applied = P/B^2, load per unit area.

  
  

Steps of MOPSO

Initialize population of particles

Initialize external archive = non-dominated solutions


Repeat until max iterations:

    For each particle:

        Compute f1(x), f2(x), ...

        Update velocity and position toward:

            - Its own best (pBest)

            - A leader chosen from archive (using diversity 	
			selection)

    Update archive with new non-dominated solutions

    Maintain diversity (crowding or grid)

Return archive (Pareto front)

The main loop of MOPSO is shown as following

%% Main loop
for it=1:MaxIt
    for i=1:nPop
        % --- Select Leader ---
        chosenLeader = SelectLeader(archive);

        if isempty(chosenLeader)
            % fallback: just use one of the current particles
            chosenLeader = particle(randi(numel(particle)));
        end

        if ~isstruct(chosenLeader)
            error('chosenLeader is not a struct, got: %s', class(chosenLeader));
        end
        if ~isfield(chosenLeader,'Position')
            error('chosenLeader has no Position field');
        end
        % --- Velocity update ---
        % particle(i).Velocity = w*particle(i).Velocity ...
        %     + c1*rand(1,nVar).*(particle(i).Best.Position - particle(i).Position) ...
        %     + c2*rand(1,nVar).*(chosenLeader.Position - particle(i).Position);
        disp('Leader position:'), disp(chosenLeader.Position);
        disp('Particle position:'), disp(particle(i).Position)
      
        diffVec = chosenLeader.Position - particle(i).Position;
        particle(i).Velocity = w*particle(i).Velocity ...
        + c1*rand(1,nVar).*(particle(i).Best.Position - particle(i).Position) ...
        + c2*rand(1,nVar).*diffVec;
        % --- Position update ---
        particle(i).Position = particle(i).Position + particle(i).Velocity;

        % Apply bounds
        particle(i).Position = max(particle(i).Position,VarMin);
        particle(i).Position = min(particle(i).Position,VarMax);

        % Evaluate
        particle(i).Cost = fobj(particle(i).Position);

        % Update personal best
        if Dominates(particle(i).Cost,particle(i).Best.Cost)
            particle(i).Best = particle(i);
        elseif ~Dominates(particle(i).Best.Cost,particle(i).Cost) && rand<0.5
            particle(i).Best = particle(i);
        end
    end

    % --- Update archive ---
    archive = UpdateArchive(archive,particle,archiveMaxSize);

    % --- Plot Pareto front ---
	
end

What are GBEST and PBEST in MOPSO framework?

The key difference in determining GBEST and PBEST in MOPSO from the single objective PSO is how to judge if the updated solution is better than the previous step. In PSO, we use objective function to measurthe improvement of the solution. However, in MOPSO, we consider non-dominant solution is the improvement. Therefore we can obtain GBEST from any solution in the archive by considering diversity of the solution i.e. crowding distance measurement (Deb, 2002) or probability based model (Mirjalili & Dong, 2019). The function to choose GBEST from archive using crowding distance technique is shown below.

function chosenLeader = SelectLeader(archive)
    if isempty(archive)
        % fallback: pick random from archive later
        chosenLeader = [];
        return;
    end

    % Build cost matrix
    n = numel(archive);
    nObj = numel(archive(1).Cost);
    Costs = zeros(n, nObj);
    for k = 1:n
        Costs(k,:) = archive(k).Cost;
    end

    % Crowding distance
    cd = CrowdingDistance(Costs);

    if all(cd==0) || sum(cd)==0
        idx = randi(n);  % pick random
    else
        P = cd/sum(cd);
        idx = RouletteWheelSelection(P);
        if isempty(idx), idx = randi(n); end  % safeguard
    end

    chosenLeader = archive(idx);
end

The RouleteWheelSelection() function is used to choose the GBEST considering the higher selection probability from the larger crowding distance i.e.

P = d/sum(d)

where d= crowding distance

c = cumsum(P)

function idx = RouletteWheelSelection(P)
    r = rand; c = cumsum(P);
    idx = find(r<=c,1,'first');
end

For each particle, PBEST is attained only when the new solution dominates the personal best record. According to the Pareto principle (Mirjalili & Dong, 2019), the function to consider whether x dominates y is shown below.

function b = Dominates(x,y)
    b = all(x<=y) && any(x<y);
end

Optimization Results

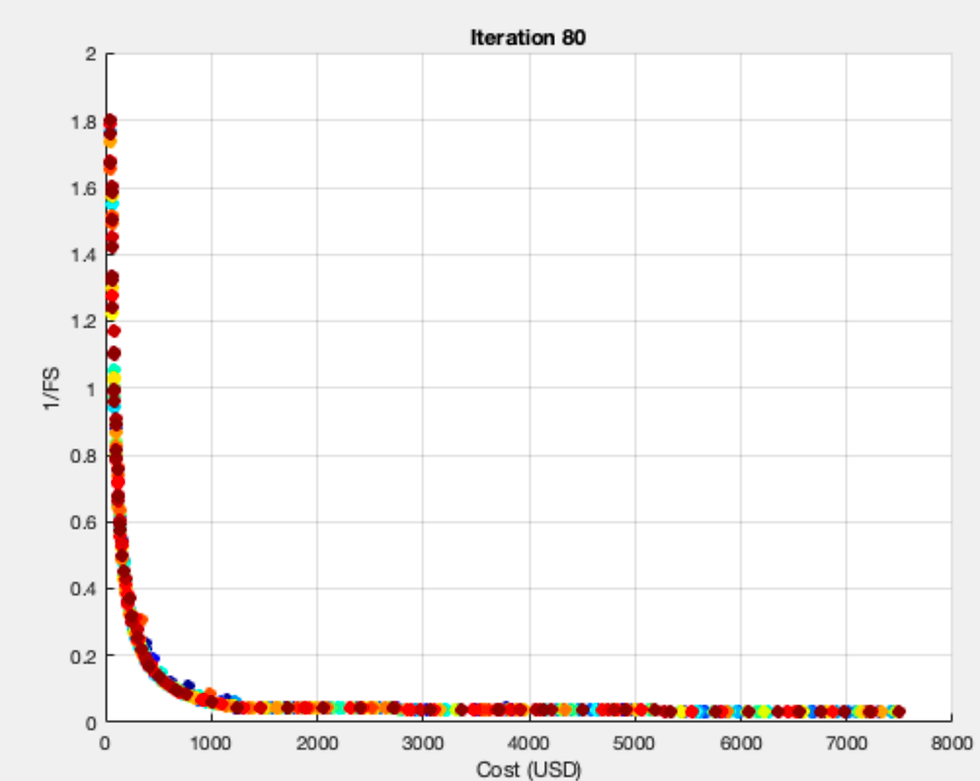
*The solutions evolve from blue (first iteration) to red (final iteration) towards

the Pareto front.

References:

Kalyanmoy Deb, Amrit Pratap, Sameer Agarwal, T. Meyarivan (2002).

A fast and elitist multiobjective genetic algorithm: NSGA-II.

IEEE Transactions on Evolutionary Computation, 6(2):182–197.

S Merjalili, JS Dong (2002), Multi-Objective Optimization using Artificial Intelligence Techniques, Springer