THEORY
Karl Terzaghi (1925) proposed the differential equation that explained the one-dimensional equation of consolidation as follows:
(Eq. 1)
The solution of (Eq. 1) can be written in series solution:
(Eq. 2)
where
(Eq. 3)
The solution in Eq.2 can be plotted as shown below
APPLICATION
Although the theory looks complicated, applying time-dependent consolidation is much simpler.
The degree of consolidation is defined as
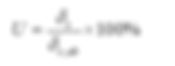
(Eq. 4)
The following steps are used for computing consolidation at time t.
For a given time t, compute Tv from Eq. 3 for each soil layer
From chart 3-3, find U from Tv
Multiply U by the final settlement (Eq.4) for each soil layer
The total settlement is the sum of settlement from each soil layer
EXAMPLE
(Coming Soon)
Q: HOW TO DETERMINE COEFFICIENT OF CONSOLIDATION (Cv)?
Two standard methods to compute the value of Cv are
- Logarithm of time method (t50)
- Square root of time method (t90)
By concept, the value of Cv is constant with time. Both methods use consolidation test data and graphical methods to find the value of Cv at a specific time t. The log of time method uses t to complete 50% of consolidation (t50), while the square root of time method uses t to complete 90% (t90) to obtain the Cv value.
REFERENCES