top of page
Search

What is Behind ETABS's Simplified C- T- Shear wall Design


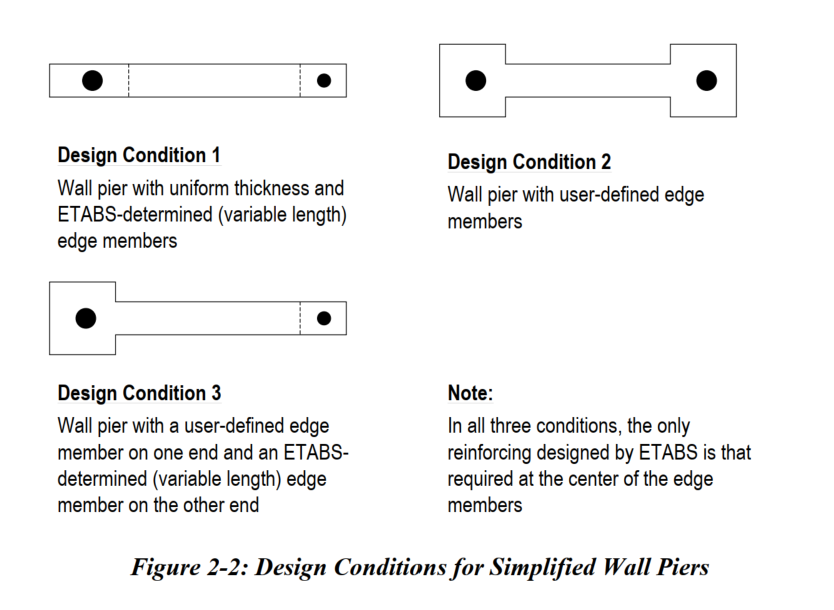
Ref. ETABS's SWD ACI318-99 Manual
Ref. ETABS's SWD ACI318-99 Manual

Based on the Shear Wall Design Manual (ACI 318-19), the Simplified C- and T-section shear wall design (Chapter 2.1.1, pages 2-2 to 2-8) involves:

  • Decomposing the applied axial force (Pu) and moment (Mu) into equivalent axial loads on left and right edge members.

  • Iteratively sizing the edge member length (B1) until the required steel area (Ast, Asc) is within max allowed ratios (PTmax, PCmax).

  • Limiting B1 such that B1 ≤ Lp/2.



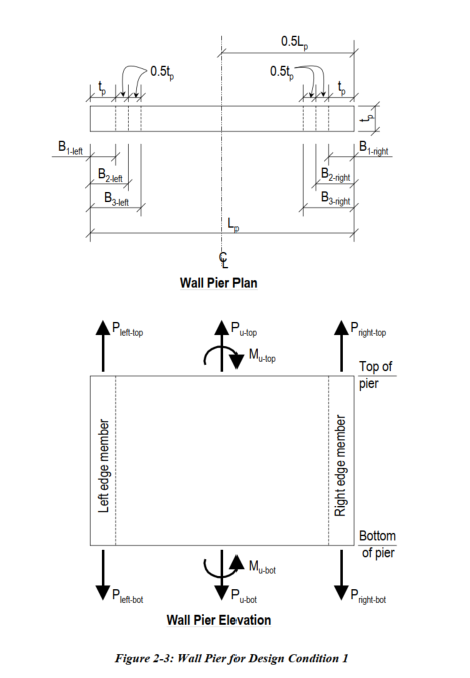
Ref. ETABS's SWD ACI318-99 Manual
Ref. ETABS's SWD ACI318-99 Manual

INPUT:
  Pu       → axial force on the pier (N or kN)

    Mu       → moment on the pier (N·mm or kN·m)

    Lp       → total horizontal length of pier (mm or m)

    tp       → thickness of wall (mm or m)

    fc       → concrete strength (MPa)

    fy       → steel yield strength (MPa)

    phi      → strength reduction factor

    PTmax    → max tension steel ratio (e.g., 0.025)

    PCmax    → max compression steel ratio (e.g., 0.02)


CONVERT all inputs to consistent units (N, mm)

SET:

    B1 = tp               → initial edge length

    max_B1 = Lp / 2       → upper bound per ACI

WHILE B1 <= max_B1:

    COMPUTE:

        P_left  = Pu/2 + Mu / (Lp - B1)

        P_right = Pu/2 - Mu / (Lp - B1)


    FOR EACH EDGE (left and right):

        IF edge axial force < 0 (tension):

            Ast = |P| / (phi * fy)

            Asc = 0

        ELSE (compression):

            Ag = B1 * tp

            Asc = max( (P - 0.85 * fc * Ag) / (phi * fy), 0 )

            Ast = 0



    CHECK:

        Ast ≤ PTmax * B1 * tp

        Asc ≤ PCmax * B1 * tp



    IF both edges pass:

        REPORT:

            Success with current B1

            Required Ast and Asc per edge

        EXIT



    ELSE:

        INCREMENT B1 by 0.5 * tp



REPORT:

    "Design failed: Steel demand exceeds max allowed even at max B1"

Here's a MATLAB example script that automates this simplified design logic for a planar T-wall section:

MATLAB Sample: Simplified C/T Shear Wall Design

% Given a wall with:
% - Pu = 1500 kN, Mu = 400 kN.m
% - Lp = 4 m, tp = 0.25 m
% - fc = 35 MPa, fy = 500 MPa
% - phi = 0.9, PTmax = 0.025, PCmax = 0.02

design_CT_wall(1500, 5000, 4, 0.25, 35, 500, 0.9, 0.025, 0.02);

function design_CT_wall(Pu, Mu, Lp, tp, fc, fy, phi, PTmax, PCmax)
% Simplified T- or C-wall design: ACI 318-19 based
% Inputs:
% Pu, Mu     - factored axial force (N), moment (N.m)
% Lp, tp     - wall length (m), thickness (m)
% fc, fy     - concrete strength (MPa), steel yield strength (MPa)
% phi        - strength reduction factor
% PTmax, PCmax - max steel ratios

% Convert to consistent units (N, mm)
Pu = Pu * 1e3; Mu = Mu * 1e6;  % to N and N.mm
Lp = Lp * 1e3; tp = tp * 1e3;

% Start iteration with edge member B1 = tp
B1 = tp;
maxB1 = Lp / 2;

while B1 <= maxB1
    % Step 1: Equivalent axial forces at edges
    P_left = Pu/2 + Mu / (Lp - B1 ); 
    P_right = Pu/2 - Mu / (Lp - B1); 

    % Step 2: Design steel areas at both edges
    % Initialize steel requirements
    Ast_left = 0; Asc_left = 0; Ast_right = 0; Asc_right = 0;
    
    % Left edge
    if P_left < 0  % tension
        Ast_left = abs(P_left) / (phi * fy ); % mm^2
    else  % compression
        Ag = B1 * tp;
        Asc_left = (P_left - 0.85 * fc * Ag) / (phi * fy );
    end

    % Right edge
    if P_right < 0
        Ast_right = abs(P_right) / (phi * fy );
    else
        Ag = B1 * tp;
        Asc_right = (P_right - 0.85 * fc * Ag) / (phi * fy );
    end
    Asc_left = max(0, Asc_left);
    Asc_right = max(0, Asc_right);

    % Step 3: Check against max ratios
    Ast_max = PTmax * B1 * tp;
    Asc_max = PCmax * B1 * tp;

    if Ast_left <= Ast_max && Asc_left <= Asc_max && ...
       Ast_right <= Ast_max && Asc_right <= Asc_max
        fprintf('\n=== Final Design ===\n');
        fprintf('Edge Member Width (B1): %.1f mm\n', B1);
        fprintf('Left Edge: Ast = %.1f mm², Asc = %.1f mm²\n', Ast_left, Asc_left);
        fprintf('Right Edge: Ast = %.1f mm², Asc = %.1f mm²\n', Ast_right, Asc_right);
        return
    end

    % Increment B1
    B1 = B1 + 0.5 * tp;
end

disp('Design failed: Required reinforcement exceeds limit even at max edge width.');
end


Output Explanation:

  • It iteratively increases the edge leg size B1 (starting from tp) until reinforcement demands are within limits.

  • Computes and prints required tension (Ast) and compression (Asc) areas at each edge.

bottom of page